Dynamika
Dynamika je další částí mechaniky, která se zabývá příčinami pohybového stavu těles. Zabývá se tedy veličinami spojenými s dynamikou pohybu, jako např. hybnost a energie.
Síla
- Síla působí na tělesa:
1. při přímém styku - tělesa se navzájem dotýkají
Nesení nákupní tašky (člověk - taška), roztlačení auta (člověk - auto), deformace míče (míč - podložka, na kterou dopadl), zpomalování padáku ve vzduchu (padák - vzduch), ...
2. prostřednictvím silového pole - tělesa nejsou ve vzájemné dotyku; síla působí prostřednictvím pole (gravitační, magnetické, elektrické, elektromagnetické, ...)
Silové působení Země na okolní předměty (kámen padající ze skály, družice obíhající kolem Země, Měsíc, …) si lze představit tak, že Země „tahá“ tyto předměty neviditelnými ručičkami k sobě. Ručičky přitom Země vystrkuje do všech směrů, takže „dosáhne“ na předměty v různých směrech i různých vzdálenostech. S rostoucí vzdáleností předmětu od Země ale síla ručiček slábne - pro Zemi je stále obtížnější předmět přitáhnout k sobě.
Síla může mít na těleso různý účinek:
1. deformační (statický) - síla má za následek deformaci tělesa
Rozbití vajíčka, přetržení nitě, prohnutí trampolíny pod artistou, ...
2. pohybový (dynamický) - síla má za následek změnu pohybového stavu tělesa
Roztlačení auta, zastavení volejbalového míče, změnu směru pohybu loďky na rybníce, …
1.První Newtonův pohybový zákon - zákon setrvačnosti:
1. setrvačnost těles v klidu - každé uvedení tělesa do pohybu
V rozjíždějícím se autobusu máme tendenci setrvat v klidu - proto padáme směrem proti směru rozjíždění.
2. setrvačnost těles v pohybu - náhlé brzdění těles, náhlá změna směru rychlosti
Zabrzdí-li prudce autobus, padáme ve směru jeho pohybu. Stejně tak (pokud se nedržíme nebo nesedíme) padáme, projíždí-li autobus rychle „ostrou“ zatáčku.
Podle prvního pohybového zákona je tedy klid a rovnoměrný přímočarý pohyb ekvivalentní. Oba dva typy pohybů jsou pohyby s nulovým zrychlením.
Vztažné soustavy, v nichž zůstávají izolovaná tělesa v klidu nebo rovnoměrném přímočarém pohybu (tedy soustavy, v nichž platí první Newtonův zákon), se nazývají inerciální soustavy. Soustavy, v nichž první pohybový zákon neplatí, se nazývají neinerciální soustavy.
Pro běžné výpočty lze považovat naši Zemi za inerciální soustavu, při letech do vesmíru lze za inerciální soustavu považovat i soustavu spojenou se Sluncem či hvězdami, neboť zrychlení těchto soustav je velmi malé.
2.Druhý Newtonův pohybový zákon - zákon síly
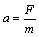. SMĚR ZRYCHLENÍ JE SHODNÝ SE SMĚREM VÝSLEDNICE SIL, TEDY 
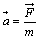.Na základě druhého pohybového zákona lze definovat jednotku síly - jeden newton: 
.
Síly udělují tělesu zrychlení podle druhého pohybového zákona nezávisle na tom, zda bylo těleso původně v pohybu či nikoliv. Zvláštním případem pak je situace, kdy výslednice sil na těleso působících je nulová. Takové těleso se pak pohybuje s nulovým zrychlením.
Budeme-li tlačit automobil silou, jejíž velikost bude stejná jako součet velikostí odporových a třecích sil působících proti pohybu, bude se automobil pohybovat rovnoměrným pohybem (tj. s nulovým zrychlením).
3.Třetí Newtonův zákon - zákon akce a reakce
KAŽDÁ DVĚ TĚLESA NA SEBE VZÁJEMNĚ PŮSOBÍ STEJNĚ VELKÝMI SILAMI OPAČNÉHO SMĚRU (JEDNÉ SÍLE SE ŘÍKÁ AKCE, DRUHÉ REAKCE). AKCE A REAKCE SOUČASNĚ VZNIKAJÍ A SOUČASNĚ ZANIKAJÍ.
Podle druhého pohybového zákona uděluje síla tělesu zrychlení. To ale nezávisí jen na síle, ale i na hmotnosti tělesa. Zrychlení těles, která na sebe vzájemně působí akcí a reakcí, proto nejsou obvykle stejně velká.
v praxi: dva kamarádi - jeden hubený a druhý zavalitý - stojí každý na svém skatu a odrazí se od sebe. Na oba působila tatáž síla, ale zavalitý se bude pohybovat podstatně pomaleji (s menším zrychlením) než hubený.
Na knihu ležící na stole (viz obr.) působí tíhová síla 
svisle dolů; tato síla (akce) vyvolá reakci stolu, který působí silou 
svisle vzhůru (protože „kniha stůl neprolomí“)
 |
4. Čtvrtý Newtonův Zákon zachování hybnosti
IZOLOVANÁ SOUSTAVA HMOTNÝCH BODŮ (TĚLES) JE SOUSTAVA, NA KTEROU NEPŮSOBÍ ŽÁDNÉ VNĚJŠÍ SÍLY RESP. V NÍŽ VÝSLEDNICE VŠECH VNĚJŠÍCH SIL PŮSOBÍCÍCH NA SOUSTAVU JE NULOVÁ.
Na základě druhého pohybového zákona tedy platí 
- časová změna hybnosti je nulová, jinými slovy hybnost soustavy se zachovává. A to je obsahem zákona zachování hybnosti:
CELKOVÁ HYBNOST VŠECH TĚLES V IZOLOVANÉ SOUSTAVĚ SE ZACHOVÁVÁ, TJ. ZACHOVÁVÁ SE SMĚR I VELIKOST CELKOVÉ HYBNOSTI. JINÝMI SLOVY: SOUČET HYBNOSTÍ VŠECH TĚLES IZOLOVANÉ SOUSTAVY JE STÁLÝ: 
.
Jednoduchý experiment lze provést s pouťovým balónkem. Nafoukněte ho a pak jej pusťte. Balónek se začne pohybovat. Příčinou pohybubalónku je proud vzduchu unikající z balónku. Před vypuštěním byla hybnost balónku a vzduchu uvnitř nulová (vzhledem k vám). Po vypuštění balónku z ruky, musí být celková hybnost balónku a vzduchu také nulová. To znamená, že co do velikosti, bude hybnost balónku stejná jako hybnost vzduchu z něj unikajícího. Obě hybnosti budou mít opačný směr.
Důležitou podmínkou platnosti zákona zachování hybnosti je izolovaná soustava. Pokud soustava, v níž budeme vyšetřovat pohyb, izolovaná nebude, zákon zachování hybnosti neplatí.
O tom se lze přesvědčit tak, že nafouknutý balónek jen částečně uvolníme z pevného sevřený mezi prsty. Vzduch z balónku bude unikat, ale balónek (stále držený prsty) se pohybovat nebude.
Zákon zachování hybnosti má praktické využití například v reaktivních motorech. Tryskami motoru unikají velkou rychlostí plyny vznikající spalováním paliva. Na základě zákona zachování hybnosti je raketa uvedena do pohybu opačným směrem. Se zákonech zachování hybnosti musí také počítat střelec, který si při výstřelu z pušky opírá zbraň o rameno.
V izolované soustavě rovněž platí zákon zachování hmotnosti:
CELKOVÁ HMOTNOST IZOLOVANÉ SOUSTAVY TĚLES JE KONSTANTNÍ.
Síly brzdící pohyb
Z praxe víme, že pokud uvedeme nějaké těleso do pohybu a přestaneme na něj působit silou, těleso se za nějakou dobu zastaví. Má-li zůstatprvní Newtonův zákon (zákon setrvačnosti) v platnosti, musí existovat nějaké vysvětlení, proč se těleso zastaví. Vysvětlení je jednoduché: během pohybu tělesa na těleso působí třecí a odporové síly, které brzdí jeho pohyb. Není tedy splněna podmínka prvního pohybového zákona.
Odporové síly vzduchu (které do této skupiny sil také patří) mají své specifické vlastnosti :
1. síla smykového tření: 1. velikost třecí síly nezávisí na obsahu styčných ploch
2. její velikost podstatně nezávisí na rychlosti
3. její velikost je přímo úměrná velikosti tlakové (normálové) síly 
kolmé k podložce, po níž se těleso pohybuje: 
, kde f je součinitel smykového tření. (Užitečné tření: pohodlná chůze, brzdění pohybu, používání pilníků, brusek, řemenic, …Nežádoucí tření: brzdění pohybu, opotřebovávání pneumatik a obuvi, nežádoucí zahřívání částí strojů, …V případě, kdy nám velké tření nevyhovuje, je nutno třecí sílu snižovat (přesným vybroušením jednotlivých částí stroje, jejich dokonalým promazáním, …).
2. síla valivého odporu: Valivý odpor vzniká vždy, když se těleso kruhového průřezu (válec, koule, …) valí po pevné podložce. Příčinou tohoto jevu je neexistence absolutně tuhého tělesa, tj. tělesa, které se nedeformuje účinkem jakkoliv velké síly. Při valení tvrdého tělesa po nedokonale pružné podložce dochází působením normálové tlakové síly k deformaci podložky. Kdyby byla podložka dokonale pružná, byla by reakce podložky 
a ležela by na stejné vektorové přímce jako normálová síla . Následkem deformace se ale působiště skutečné reakce 
posune o vzdálenost 
kupředu. Pro velikost síly , kterou udržíme těleso v rovnoměrném přímočarém pohybu, pak platí 
. Pro malé úhly 
je 
. Podle obr. 42 je R poloměr tělesa s kruhovým průřezem a platí 
. Pro velikost síly 
tedy dostáváme 
.
 |
3. síla vláknového tření:Smýká-li se lano po nehybné válcové ploše (viz obr. 44), vzniká mezi lanem a válcovou plochou třecí síla, která je příčinou vláknového tření. Velikost této síly závisí na úhlu opásání lana 
a na součiniteli smykového tření f mezi lanem a válcovou plochou.
Úhel opásání udává, na jaké části obvodu válcové plochy se lano této plochy dotýká!
 |
| Obr. 44 |
Tento druh tření vzniká při spouštění nebo zvedání kbelíku s maltou při stavbě domu pomocí lana, které je vedeno přes vodorovnou válcovou trubku, kterou zedníci umístili v okně domu. S tímto druhem tření se setkáváme i u videorekordéru, promítačky, … Při vložení kazety do videorekordéru je páska vytažena z kazety a přivedena k čtecí resp. záznamové hlavě videa. Vytažení pásky realizují „kolíčky“ ve tvaru válců. Kolem nich je páska ovinuta a postupně tažena z kazety. Ačkoliv se kolíčky mohou otáčet kolem vlastní osy, čím snižují vláknové tření mezi nimi a páskou, může se páska po kolíčku i smýknout.
Dostředivá síla
V kinematice byl popsán pohyb hmotného bodu po kružnici. Při rovnoměrném pohybu hmotného bodu po kružnici má rychlost hmotného bodu stále stejnou velikost, ale mění se její směr. V důsledku toho má hmotný bod dostředivé zrychlení 
, pro jehož velikost platí 
, kde r je poloměr kružnice, v velikost rychlosti hmotného bodu a 
jeho úhlová rychlost.
Podle druhého Newtonova zákona je příčinou zrychlení hmotného bodu vždy nějaká síla, která má stejný směr jako zrychlení. V tomto případě se jedná tedy o sílu dostředivou 
, pro jejíž velikost platí 
.
Zkuste si na vodorovný stůl položit kuličku a opatrně do ní cvrnknout prstem. A přitom na ní působit silou tak, aby se kulička pohybovala po kružnici. Není to lehké …
Směr dostředivé síly je kolmý na směr okamžité rychlosti hmotného bodu. Jejím pohybovým účinkem na hmotný bod je změna směru rychlosti hmotného bodu a zakřivení jeho trajektorie do tvaru kružnice.
Dostředivá síla může mít původ v libovolném vzájemném silovém působení dvou těles. Tato síla může být realizována:
Přivažte na kousek provázku kuličku (ping-pongový míček, …), provázek jedním prstem přimáčkněte ke stolu a druhou rukou uveďte kuličku (míček) do pohybu. Aniž byste to chtěli, bude se kulička (míček) pohybovat po kružnici.
2. gravitační silou - pohyb družic kolem Země, pohyb planet kolem Slunce, …
3. magnetickou silou - vychylování elektronů v obrazovce televizoru, …
Přestane-li dostředivá síla na těleso působit, pohybuje se těleso dále ve směru tečny ke kružnici
Jiskry odlétající od brusného kotouče, hod kladivem, vrh koulí, …
Působí-li na těleso, které koná rovnoměrný pohyb po kružnici, více sil, je dostředivá síla výslednicí všech těchto sil.